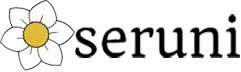Seruni.id – Geometri adalah salah satu materi yang terdapat di dalam pelajaran matematika. Dan bangun datar merupakan topik yang ada di dalamnya. Dengan mempelajari tentang bangun datar, kita bisa menerapkannya untuk menyelesaikan permasalahan dalam kehidupan sehari-hari. Lantas, apa itu bangun datar? Mari simak penjelasannya berikut ini, yuk!
Pengertian Bangun Datar
Sebelum mengenal ciri-ciri dan rumusnya, kita harus tahu dulu nih, apa sih bangun datar itu? Bangun datar adalah suatu bidang datar yang dibatasi dengan gari-garis lurus atau garis lengkung. Lebih tepatnya, bangun datar merupakan bangunan dengan bidang rata yang terbentuk dari dua dimensi, yakni panjang dan lebar. Selain itu, bangun datar juga tidak memiliki tinggi atau ketebalan.
Banguan datar terdiri dari berbagai bentuk, di antaranya lingkaran, persegi, persegi panjnag, jajar genjang, belah ketupat, segitiga, segi lima (pentagon), dan trapesium. Masing-masing bentuk tersebut memiliki ciri dan rumus yang berbeda.
Macam-macam Bangun Datar
Bangun datar memiliki 8 bentuk yang harus kamu ketahui. Nah, berikut ini, Seruni akan memberikan gambar bangun datar beserta ciri-ciri serta rumusnya yang bisa kamu pelajari.
1. Lingkaran

Tahukah kamu? Ternyata bentuk lingkaran termasuk ke dalam salah satu bangun datar, loh. Lingakaran sendiri terdiri dari semua titik dalam bidang dengan jarak tertentu dari titik pusat. Semua titik yang berada di dalam persekitaran lingkaran memiliki jarak yang sama. Jarak tersebut diberi nama r yang dikenal dengan sebutan radius atau jari-jari. Bangunan tersebut tidaklah tersusun dari garis lurus, melainkan dari kurva. Sehingga berbeda dengan poligon atau bahan bukan termasuk jenis poligon.
Ciri-ciri Lingkaran
- Terdapat r (jari-jari) atau jarak tepi garis ke ttik pusat.
- Memiliki sudut 180 derajat.
- Memiliki sistem lipat dan simetri putar yang jumlahnya tak terhingga.
- Diameternya membagi bangunan menjadi dua sisi yang seimbang.
Rumus Lingkaran
- Luas: L = π × r × r
L = ¼ × π × d × d - Keliling: K = π × d
K = π × 2r - Phi: π = 22/7
π = 3,14 - Jari-jari: r = d/2
- Diameter: d = 2r
Keterangan:
- L: Luas
- K: Keliling
- π: 22/7 atau 3,14
- r: Jari-jari
- d: Diameter
Contoh Soal
Apabila sebuah lingkaran memiliki jari-jari dengan panjang 21 cm, lalu berapakah keliling dan luas lingkaran tersebut?
Penyelesaian:
K = π × 2r
K = 22/7 × 2 × 21
K = 22 × 2 × 3
K = 22 × 6
K = 132 cm
L = π × r × r
L = 22/7 × 21 × 21
L = 22 × 3 × 21
L = 66 × 21
L = 1386 cm²
Jadi, keliling lingkaran tersebut adalah 132 cm dengan luas 1386 cm²
2. Persegi

Bujur sangkar alias persegi adalah salah satu bangun datar dengan dua dimensi. Bangunan ini terbentuk dari empat buah rusuk dengan ukuran dan sisi yang sama panjang. Selain itu, persegi juga memiliki empat sudut siku-siku. Dapat kita simpulkan, bahwa bangun datar yang satu ini, memiliki sisi-sisi yang sama panjang dan sudut yang sama besar.
Ciri-ciri Bangunan Persegi
- Semua sisinya sama panjang
- Memiliki diagonal yang sama panjang. Namun, keduanya saling berpotongan tegak lurus, sehingga membagi dua sama panjang.
- Terdapat empat sumbu simetri, yakni putar dan lipat.
- Setiap sudutnya memiliki besar 90 derajat.
Rumus Persegi
- Luas Persegi: L = s × s
L = (K/4)² - Keliling: K = 4s
- Diagonal: d = s × √2
- Sisi: s = √L
s = K÷4
s = d÷√2
Keterangan
- L: Luas
- K: Keliling
- s: Sisi
- d: Diagonal
Contoh Soal
Sebuah persegi memiliki panjang sisi 13 cm, berapakah luas dan keliling persegi tersebut?
Penyelesaian:
Diketahui s = 13 cm
L = s × s
L = 13 × 13
L = 169 cm²
K = 4s
K = 4×13
K = 52 cm
Luas dari persegi tersebut adalah 169 cm² dan kelilingnya adalah 52 cm.
3. Persegi Panjang

Bangun datar berikutnya adalah persegi panjang, yaitu bangunan dengan keempat sudut siku-siku dan sisi yang berhadapan sama panjang. Namun, persegi panjang dibatasi dengan sisi-sisi. Bangun datar dua dimensi ini, terdiri dari panjang dan lebar dengan ukuran yang berbeda.
Ciri-ciri Persegi Panjang
- Memiliki empat sudut dengan besaran 90 derajat (siku-siku).
- Terdiri dari dua sumber simeteri lipat dan putar.
- Memiliki dua diagonal alias garis melintang yang sama panjang.
- Dua pasang sisinya sejajar dan sama panjang.
Rumus Persegi Panjang
- Luas: L = p × l
- Keliling: K = 2 (p + l)
- Diagonal: d = √(p² + l²)
- Panjang: p = L ÷ l
p = K ÷ 2 – l
p = √ (d² – l²) - Lebar: l = L ÷ p
l = K ÷ 2 – p
l = √(d² – p²)
Keterangan
- L: Luas
- K: Keliling
- p: Panjang
- l: Lebar
- d: Diagonal
Contoh Soal
Cobalah hitung berapa keliling dan luas persegi yang memiliki panjang sisi 65 cm dan 30 cm?
Penyelesaian:
Diketahui p = 65 cm dan l = 30 cm
K = 2(p+l)
K = 2 (65+30)
K = 2 × 95
K = 190 cm
L = p×l
L = 65×30
L = 1950 cm²
Keliling persegi panjang tersebut adalah 190 cm dengan luas 1950 cm².
4. Segitiga
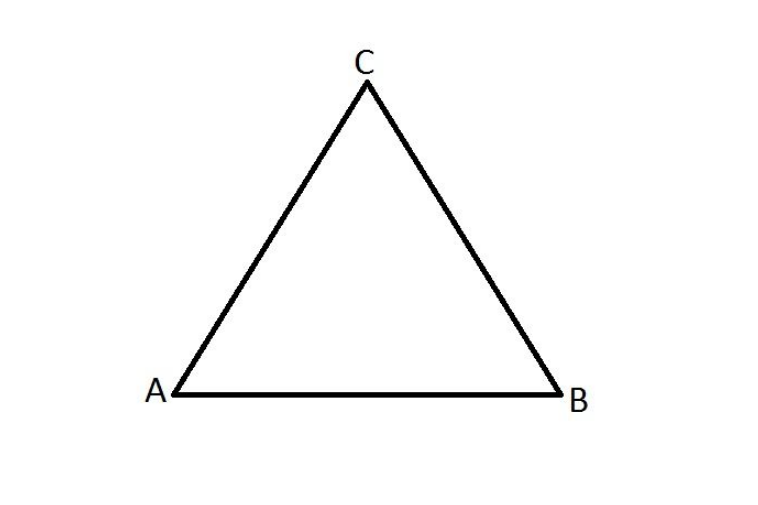
Mungkin kamu tidak asing lagi dengan bangun datar yang satu ini. Bentuknya yang mengerucut ini adalah bangun datar segitiga, yang dibangun dari tiga sisi berbentuk garis lurus. Maka dari itu, segitiga memiliki tiga sudut, yakni di atas, kanan, dan kiri.
Ciri-ciri Segitiga
- Terdapat tiga buah sisi.
- Memiliki tiga buah titik sudut.
- Terdapat tiga sisi dan tiga sudut.
- Semua sudut dan sisinya bisa berbeda ukuran.
- Selain itu, ada beberapa ciri utama dari ketiga jenis banguan datar segitiga, yakni:
- Adanya tiga sisi yang sama panjang pada segitiga sama sisi.
- Segitiga sama kaki memiliki tiga sisi dengan dua sisi yang sama panjang dengan sudut 60 derajat.
- Terdapat tiga sisi dengan 90 derajat pada segitiga siku-siku.
Rumus Segitiga
- Luas: L = ½ × a × t
L = √(s × (s-a) × (s-b)× (s-c)) - Keliling: K = a+b+c
K = Jumlah Semua Sisi - Alas: a = 2L ÷ t
- Tinggi (t): t = 2L ÷ a
- Keterangan
- L: Luas
- K: Keliling
- s: 1/2 Keliling
- a: Alas segitiga
- t: Tinggi segitiga
- b: Sisi segitiga
- c: Sisi segitiga
5. Segi Lima (Pentagon)
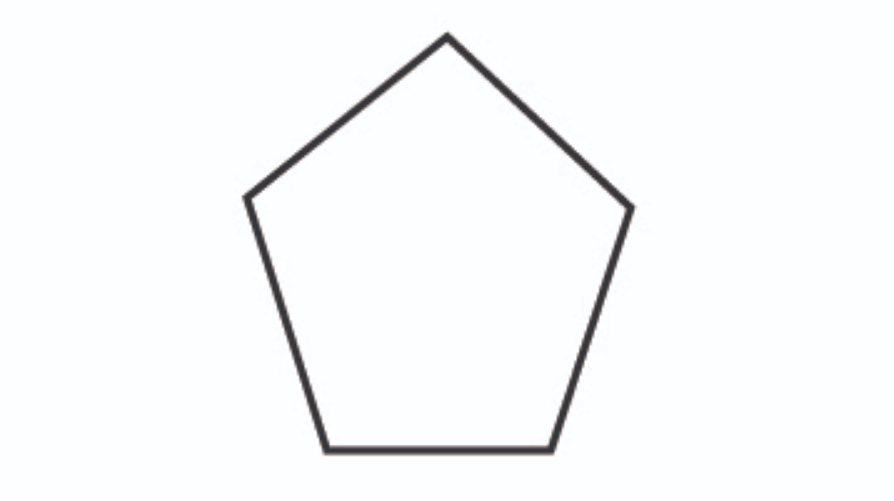
Bangun datar berikutnya adalah segi lima atau pentagon. Istilah tersebut, biasanya merujuk pada segi lima sama sisi, di mana sisinya saling berhubungan.
Ciri-ciri Segi Lima
- Terdapat lima sisi yang sama panjang dan beraturan.
- Setiap garis yang beraturan, terdapat lima sudut yang sama besar, ykani 108 derajat.
- Terdiri dari lima sumbu simetri.
- Jika dijumlahkan, setiap sdutu pada segi lima berjumlah 540 derajat.
6. Trapesium
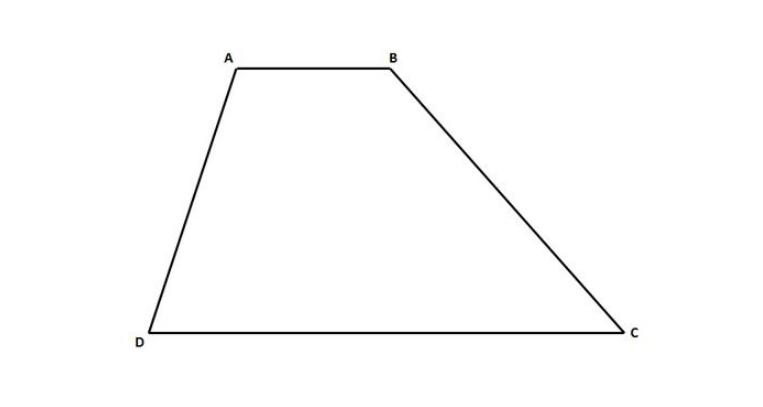
Trapesium adalah bangun datar dua dimensi yang dibentuk dari empat rusuk. Dua rusuk di antaranya saling sejajar, tetapi panjangnya tidak sama. Namun, ada pula trapesium yang ketiga rusuknya membentuk sudut tegak lurus pada rusuk-rusuk sejajar. Trapesium yang memiliki sisi tegak biasa dikenal dengan sebutan trapesium siku-siku.
Ciri-ciri Trapesium
- Memiliki empat sisi denagn dua sisi sejajar.
- Terdapat empat sudut, di mana dua sudut saling berdekatan dengan jumlah 180 derajat.
- Panjang sisinya tidak selalu berukuran sama.
- Pada trapesiumsama kaki, garis kakinya memiliki sama panjang yang sama dan sejajar.
Rumus Trapesium
- Luas: L = ½ × (a+b) × t
- Keliling: K = a + b + c + d
- Tinggi: t = 2L / (a+b)
- Sisi a: a = 2L / t – b
a = K – b – c – d - Sisi b: b = 2L / t – a
b = K – a – c – d - Sisi c: c = K – a -b – d
- Sisi d: d = K – a – b – c
7. Jajar Genjang
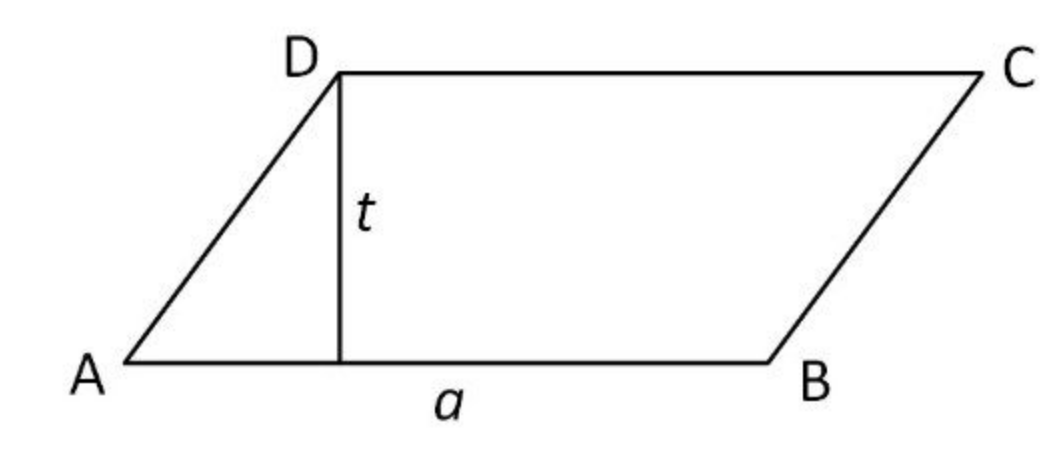
Sekilas, bentuknya memang hampir mirip dengan persegi. Sebab, bangun datar jajar genjang, memang dibentuk dengan empat sisi yang sama panjang. Hanya saja yang membeakan adalah, jajar genjang tampak lebih miring.
Ciri-ciri Jajar Genjang
- Tidak memiliki simetri lipat.
- Memiliki simetri putar tingkat dua.
- Sudut yang saling berhadapan memiliki ukuran yang sama besar.
- Terdapat empat sisi serta empat sudut.
Rumus Jajar Genjang
- Luas: L = a × t
- Keliling: K = 2 (a + b)
- Sisi alas: a = (K/2) – b
a = L/t - Tinggi: t = L/a
- Sisi miring: b = (K/2) – a
Keterangan
- L: Luas
- K: Keliling
- a: Sisi alas
- t: Tinggi
- b: Sisi miring
8. Belah Ketupat
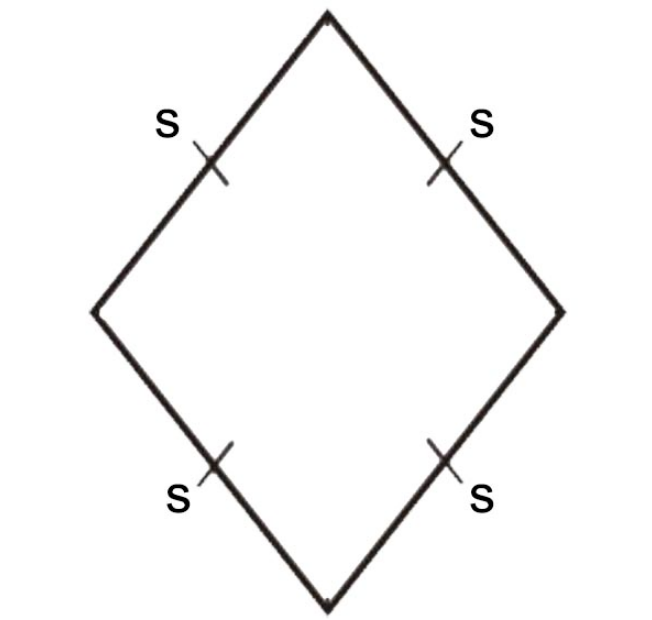
Nama bangun datar yang berikutnya adalah belah ketupat. Belah ketupat adalah bangun datar dua dimensi yang dibentuk dari empat sisi yang sama panjang. Pada badan belah ketupat, bisa membentuk garis lurus diagonal yang menghasilkan siku yang sama besar (saling berhadapan).
Ciri-ciri Belah Ketupat
- Keempat sisinya sama panjang.
- Adanya 2 diagonal yang saling tegak lurus.
- Diagonal 1 (d1) dan diagonal 2 (d2) pada belah ketupat saling tegak lurus membentuk sudut siku-siku (90°).
- Sudut yang saling berhadapan sama besar.
- Pada belah ketupat sudut yang berhadapan memiliki besar yang sama.
- Jumlah keempat sudutnya 360º.
- Adanya 2 sumbu simetri yaitu tepat pada diagonalnya.
- Terdapat pula simetri putar tingkat 2.
- Memiliki 4 buah sisi dan 4 titik sudut.
Rumus Belah Ketupat
- Luas: L = ½ × d1 × d2
- Diagonal 1: d1 = 2L / d2
- Diagonal 2: d2 = 2L / d1
- Keliling: K = 4s
- Sisi: s = K/4
s = √((½d1)² + (½d2)²)
Keterangan
- L: Luas
- K: Keliling
- d1: Diagonal 1
- d2: Diagonal 2
- s: Sisi
Contoh Soal
Berapakah keliling dan luas belah ketupat yang memiliki panjang diagonal 6 cm dan 8 cm serta panjang sisinya 5 cm?
Penyelesaian:
Diketahui d1 = 6 cm, d2 = 8 cm, dan s = 5 cm
L = ½ × d1 × d2
L = ½ × 6 × 8
L = 3 × 8
L = 24 cm²
K = 4s
K = 4 × 5
K = 20 cm
Jadi, luas belah ketupat tersebut adalah 24 cm² dan kelilingnya adalah 20 cm.
Baca Juga: Cara Menghitung Pecahan Campuran dengan Mudah!
Itulah delapan bentuk bangun datar beserta ciri-ciri dan rumus yang bisa kamu pelajari. Tidak sulit untuk menemukan bangun datar karena bangun datar dua dimensi itu berada di sekitar kita. Semua bangun datar yang ditemui juga bisa diukur kok. Semoga bermanfaat!